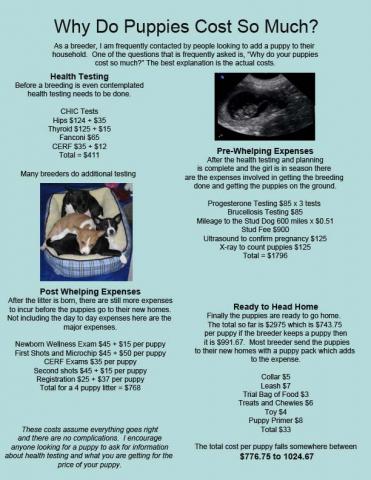
Why Do Puppies Cost So Much?
-
Ivoss, well done! It's sad that a breeder has to actually itemize this to make a prospective buyer understand, but if that's what it takes, that's what it takes. I would also venture a guess that people who complain about the pricing have not spoken with the breeder very much - they have not gotten a feeling or understanding of what is involved in proper breeding practices.
-
It is true that many haven't taken the time to talk to breeders and understand the Why of price. The problem with most is that as soon as they hear the price the move on looking for the "bargain" without understanding that what they are likely to find is no bargain just a bunch of costs down the line. The itemized cost doesn't even begin to show everything that goes into a litter either. It is very frustrating when price is the only factor being considered.
-
Very nice and def. informative…you shouldn't have to tally it up though...
Sent from my rockin' Samsung Vibrate via Tapatalk.
-
Funny, isn't it, how people will brag about how much they paid for a puppy bought at a petstore, but then try to haggle with a breeder over the price? I think your breakdown of the costs is quite reasonable, and you made a nice page to show to argumentative people to explain WHY the costs is barely breakeven. With Linda and my Thymely litter, I wryly thought to myself after all the costs were tallied, Ra was "only" a $200 pup. In other words, we didn't break even. But, we have some very nice pups, and the pet puppies are in wonderful homes.
Katy
-
Katy, that is pretty much how my husband and I feel. As long as we aren't more in the hole than we would have been buying a puppy then we did pretty good. Unfortunately, that hasn't been the case recently. The Silken Windhound folks remember and fondly refer to L'Ox as the "most expensive basenji puppy" because he is a frozen semen puppy born via c-section and was a singleton so no other puppies to spread the cost over. We didn't ever do a real tally for what his actual cost was, I don't really want to know.
-
Lisa, did you include removal of dew claws in the wellness puppy check? I didn't see that on your breakdown.
And yes, it is very fustrating when talking to potential puppy people and they "challenge" the price… or that is the first and only consideration they have... Many will say "but I don't want a show dog" or "I would take the runt".... and honestly, when you get a puppy from a responsible breeder, rarely is there a "runt" or one that could not be shown...
-
Yes, the $15 per puppy is for the dewclaws in the newborn wellness check.
And trust me everyone… many Vets charge way more than is in Lisa's tally... take that tally plus at least 10% would be my Vets charges.
And Kipawa.... if we ever added in our time... the prices would be out of sight...:eek:
-
It isn't just pet people. People looking for show and performance dogs too. Recently, I have encountered several people, pet and show, who think I should just be grateful they would even consider a puppy from me.
Oh boy, good thing I am not a breeder (never plan to be, I leave it to the experts). If I was a breeder and someone even slightly indicated that I should be grateful they are considering one of my dogs, that person would be scratched off my list so fast. I'd probably also contact my other breeder colleagues to advise them of this person's attitude. To me, if someone is acting like that prior to getting a dog, their actions afterwards would certainly be no better, and I could see where the dog would suffer being with such an owner.
-
I think people love to brag about how much they paid for everything, but it is also natural for people to try, at least, to get a lower price on the things they buy. the sad thing is that normally, the care people give to the things they buy depends on how much they paid for them, notice I say "things" because I think that's how a lot of these people think about anything that they are buying, even if it is alive. Ive had people here say things like, " that operation will cost more than the dog!!! Just get another one!! ".. You know, honestly I don't waste my time even arguing with people like that, if you can't see the difference between a dog and , say a car, then you know it's like speaking a different language.
-
I have noticed that dogs here get more expensive depending on their popularity, for example French bulldogs are really popular here now and I have seen them for sale, at pet stores, without "papers" meaning who knows, for the equivalent of 1000 US dollars.
Pet stores sell " pure breed" dogs with no papers, which is funny because, there comes a point when the dogs aren't even close to the breed anymore, like chihuahuas, for example, everyone in this country owns a chihuhua, but when you compare them to akc chihuhuas, they are two different dogs. The Dominican version has a very small head and long thing snout, like a whippet!!!! -
Not declaw, dewclaws, the "thumbs". I have them removed at a day old because when done that young it is very simple procedure and not traumatic for the puppy. Dewclaw injuries can be quite bad and quite expensive and major surgery for the dog. Since I course with my dogs and on several natural fields that are not a quick drive to an ER vet, I rather do it early instead of risking it later.
-
Not declaw, dewclaws, the "thumbs". I have them removed at a day old because when done that young it is very simple procedure and not traumatic for the puppy. Dewclaw injuries can be quite bad and quite expensive and major surgery for the dog. Since I course with my dogs and on several natural fields that are not a quick drive to an ER vet, I rather do it early instead of risking it later.
And while it is not a practice to remove dew claws especially "across the pond" it is pretty much common practice here. It does become a matter of personal preference. I have seen many dew claw injuries… and they are not pretty .... and while we have a short haired breed that you can clearly see the dew claws, long hair breeds you can not.. therefore I have also seen many dew claws not kept trimmed that grow around and back into the skin...